Panel Data Analysis: A Guide for Nonprofit Studies

The growing push in nonprofit studies toward panel data necessitates a methodological guide tailored for nonprofit scholars and practitioners. Panel data analysis can be a robust tool in advancing the understanding of causal and/or more nuanced inferences that many nonprofit scholars seek. This study provides a walk-through of the assumptions and common modeling approaches in panel data analysis, as well as an empirical illustration of the models using data from the nonprofit housing sector. In addition, the paper compiles applications of panel data analysis by scholars in leading nonprofit journals for further reference.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime

Buy Now

Price includes VAT (France)

Instant access to the full article PDF.

Rent this article via DeepDyve

Similar content being viewed by others

Panel Data Analysis

Panel Data Analysis

Non-linear Panel Data Models

Explore related subjects

Notes

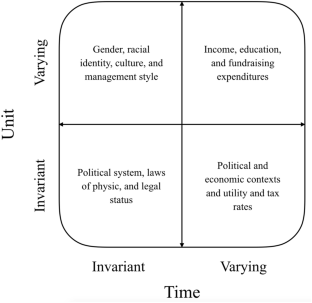
Regarding different types of data, in general, time-series data refers to a collection of observations made chronologically on one subject, for instance, historical stock prices of one firm. In this case, in order to have enough variation, the length of a time series is an important determinant of the usefulness of such data, panel data, as we mentioned in the paper, entail observations made on the same sample of subjects over time. The difference here is in the data structure. Compared with time-series data, panel data have more than one cross-sectional subject. Accordingly, both its length (i.e., number of time periods) and its width (i.e., number of cross-sectional subjects) jointly decide the usefulness of a panel dataset. Additionally, some studies also use the term time-series cross-sectional (TSCS) data to refer to panel data (Lewis-Beck et al., 2004), while some others suggest that TSCS data have comparatively fewer cross-sectional subjects than panel data (see Bell & Jones, 2015). As for the term longitudinal data, researchers often use it interchangeably with the term panel data (Frees, 2004).

Here, a necessary yet challenging sampling strategy in panel data analysis is to keep track of the same sampled subjects until the completion of data collection, as attrition of subjects out of the sample could lead to incorrect inferences (Baltagi, 2008).

Here, we acknowledge that it is common for nonprofit scholars to choose other publication outlets such as Journal of Public Administration Research and Theory (e.g., Cheng, 2018; de Wit & Bekkers, 2017) and Public Performance & Management Review (e.g., Pandey & Johnson, 2019). Given the broad coverage of these journals, however, we decided to narrow our focus on VOLUNTAS, NML, and NVSQ, which focus solely on nonprofit studies.

In practice, the presence of different levels of multicollinearity is common given the implicit and/or explicit interconnectedness of many variables in social sciences. The disadvantage of having multicollinearity is that it could lead to relatively large estimated standard errors for the coefficient estimates of independent variables that are correlated with others, which would undermine their statistical significance (Allen, 1997).

Here, it is important to acknowledge that directly adding an LDV as an independent variable could violate the OLS assumption that independent variables do not correlate with the error term. This is because the error term is supposed to encapsulate all the variation that is left in the dependent variable but are not explained by the independent variable(s). An LDV is thus likely to correlate with such remaining variation as it represents the variation in the DV that is from the previous period. This issue would be further complicated if the model specification includes panel-specific error terms such as FE terms (Zhu, 2013). In this case, we do not recommend directly adding an LDV to account for the dynamics process. We introduce this approach because it is our intention to provide the basic assumptions and modeling approaches that are involved in panel data analysis. To deal with such potential correlations that an LDV might induce, however, researchers could rely on instrumentation techniques such as a second-order LDV (the DV that is two periods before the current one; Anderson & Hsiao, 1981) or the generalized method of movements (GMM) estimator proposed by Arellano & Bond (1991).

References

• Allen, M. P. (1997). The problem of multicollinearity. In Understanding regression analysis, pp. 176–180. Springer. Doi: https://doi.org/10.1007/978-0-585-25657-3_37
• Amirkhanyan, A. A., Kim, H. J., & Lambright, K. T. (2009). Faith-based assumptions about performance: Does church affiliation matter for service quality and access? Nonprofit and Voluntary Sector Quarterly,38(3), 490–521. https://doi.org/10.1177/0899764008320031ArticleGoogle Scholar
• Anderson, T. W., & Hsiao, C. (1981). Estimation of dynamic models with error components. Journal of the American Statistical Association,76(375), 598–606. https://doi.org/10.2307/2287517ArticleGoogle Scholar
• Arellano, M. (2003). Panel data econometrics. Oxford university press. https://books.google.com/books/about/Panel_Data_Econometrics.html?id=--QBWO67VjsC
• Arellano, M., & Bond, S. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. The Review of Economic Studies,58(2), 277–297. https://doi.org/10.2307/2297968ArticleGoogle Scholar
• Bae, K. B., & Sohn, H. (2018). Factors contributing to the size of nonprofit sector: Tests of government failure, interdependence, and social capital theory. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations,29(3), 470–480. https://doi.org/10.1007/s11266-017-9888-3ArticleGoogle Scholar
• Baltagi, B. H. (2008). Econometric analysis of panel data. John Wiley & Sons. Google Scholar
• Baltagi, B. H., Bresson, G., & Pirotte, A. (2003). Fixed effects, random effects or Hausman–Taylor?: A pretest estimator. Economics Letters,79(3), 361–369. https://doi.org/10.1016/S0165-1765(03)00007-7ArticleGoogle Scholar
• Bartels, B. (2015). Beyond ‘fixed versus random effects’: A framework for improving substantive and statistical analysis of panel, TSCS, and multilevel data. In R. Franzese (Ed.), Quantitative research in political science. SAGE Publications Ltd. https://us.sagepub.com/en-us/nam/quantitative-research-inpolitical-science/book243299
• Beckman, C. M., & Burton, M. D. (2008). Founding the future: path dependence in the evolution of top management teams from founding to IPO. Organization Science,19(1), 3–24. https://doi.org/10.1287/orsc.1070.0311ArticleGoogle Scholar
• Bell, A., & Jones, K. (2015). Explaining fixed effects: Random effects modeling of time-series cross-sectional and panel data. Political Science Research and Methods,3(1), 133–153. ArticleGoogle Scholar
• Bromley, P., Schofer, E., & Longhofer, W. (2018). Organizing for education: A cross-national, longitudinal study of civil society organizations and education outcomes. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations,29(3), 526–540. https://doi.org/10.1007/s11266-018-9979-9ArticleGoogle Scholar
• Brooks, A. C. (2000). Public subsidies and charitable giving: Crowding out, crowding in, or both? Journal of Policy Analysis and Management,19(3), 451–464. https://doi.org/10.1002/1520-6688(200022)19:3%3c451::AID-PAM5%3e3.0.CO;2-EArticleGoogle Scholar
• Bun, M. J., & Sarafidis, V. (2013). Dynamic panel data models. UvA-Econometrics Discussion Paper, 1.
• Calabrese, T. D. (2011). The Accumulation of Nonprofit Profits: A Dynamic Analysis. Nonprofit and Voluntary Sector Quarterly,41(2), 300–324. https://doi.org/10.1177/0899764011404080ArticleGoogle Scholar
• Cameron, A. C., & Trivedi, P. K. (2010). Microeconometrics using stata, Vol. 2. Stata press College Station.
• Cheng, Y. (2018). Nonprofit spending and government provision of public services: Testing theories of government-nonprofit relationships. Journal of Public Administration Research and Theory,29(2), 238–254. https://doi.org/10.1093/jopart/muy054ArticleGoogle Scholar
• Clark, T. S., & Linzer, D. A. (2015). Should I use fixed or random effects? Political Science Research and Methods,3(2), 399–408. ArticleGoogle Scholar
• Cooper, H. M. (1989). Integrating research: A guide for literature reviews. Sage Publications. Google Scholar
• Coupet, J. (2018). Exploring the link between government funding and efficiency in nonprofit colleges. Nonprofit Management and Leadership,29(1), 65–81. https://doi.org/10.1002/nml.21309ArticleGoogle Scholar
• Coupet, J., & Berrett, J. L. (2019). Toward a valid approach to nonprofit efficiency measurement. Nonprofit Management and Leadership,29(3), 299–320. https://doi.org/10.1002/nml.21336ArticleGoogle Scholar
• David, R. J., & Han, S. (2004). A systematic assessment of the empirical support for transaction cost economics. Strategic Management Journal,25(1), 39–58. ArticleGoogle Scholar
• De Los Mozos, I. S. L., Rodríguez Duarte, A., & Rodríguez Ruiz, Ó. (2016). Resource dependence in non-profit organizations: Is It harder to fundraise if you diversify your revenue structure? VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations,27(6), 2641–2665. https://doi.org/10.1007/s11266-016-9738-8ArticleGoogle Scholar
• de Wit, A., & Bekkers, R. (2017). Government support and charitable donations: A meta-analysis of the crowding-out hypothesis. Journal of Public Administration Research and Theory,27(2), 301–319. https://doi.org/10.1093/jopart/muw044ArticleGoogle Scholar
• Diebold, J., & Coggburn, J. D. (2018). The determinants and opportunity costs of external management fees for state-administered pension plans. Public Budgeting and Finance,38(4), 3–31. https://doi.org/10.1111/pbaf.12207ArticleGoogle Scholar
• Einolf, C. J. (2017). Parents’ charitable giving and volunteering: Are they influenced by their children’s ages and life transitions? Evidence from a longitudinal study in the United States. Nonprofit and Voluntary Sector Quarterly,47(2), 395–416. https://doi.org/10.1177/0899764017737870ArticleGoogle Scholar
• Elhorst, J. P. (2003). Specification and estimation of spatial panel data models. International Regional Science Review,26(3), 244–268. https://doi.org/10.1177/0160017603253791ArticleGoogle Scholar
• Faulk, L., & Derrick-Mills, T. (2015). Shaping the Future of Nonprofit Data. Shaping the Future of Nonprofit Data. https://www.american.edu/spa/news/shaping-future-of-nonprofit-data-07062015.cfm
• Frees, E. W. (2004). Longitudinal and panel data: Analysis and applications in the social sciences. Cambridge University Press. BookGoogle Scholar
• Galaskiewicz, J., & Bielefeld, W. (1998). Nonprofit Organizations in an Age of Uncertainty: A Study of Organizational Change. A. de Gruyter.
• Garson, G. D. (2013). Longitudinal Analysis. Statistical Associates Publishers. Google Scholar
• Glanville, J. L., Paxton, P., & Wang, Y. (2015). Social capital and generosity: A multilevel analysis. Nonprofit and Voluntary Sector Quarterly,45(3), 526–547. https://doi.org/10.1177/0899764015591366ArticleGoogle Scholar
• Greene, W. H. (2003). Econometric Analysis (5th, illustrated ed.). Prentice Hall. https://books.google.com/books?id=JJkWAQAAMAAJ
• Grossman, A., & Rangan, V. K. (2001). Managing multisite nonprofits. Nonprofit Management and Leadership,11(3), 321–337. https://doi.org/10.1002/nml.11306ArticleGoogle Scholar
• Habitat for Humanity. (2014, November 11). HUD awards $4.2 million capacity building grant to Habitat for Humanity. https://www.habitat.org/newsroom/11-11-2014-HUD-Capacity-Building
• Habitat for Humanity. (2020). Our mission, vision, and principles. https://www.habitat.org/about/mission-and-vision
• Halaby, C. N. (2004). Panel models in sociological research: Theory into practice. Annual Review of Sociology,30(1), 507–544. https://doi.org/10.1146/annurev.soc.30.012703.110629ArticleGoogle Scholar
• Hannan, M. T., & Freeman, J. (1984). Structural inertia and organizational change. American Sociological Review,49(2), 149–164. https://doi.org/10.2307/2095567ArticleGoogle Scholar
• Hausman, J. A. (1978). Specification tests in econometrics. Econometrica,46(6), 1251–1271. https://doi.org/10.2307/1913827ArticleGoogle Scholar
• Heist, H. D., & Vance-McMullen, D. (2019). Understanding donor-advised funds: how grants flow during recessions. Nonprofit and Voluntary Sector Quarterly, 48(5), 1066–1093. https://doi.org/10.1177/0899764019856118. ArticleGoogle Scholar
• Heutel, G. (2014). Crowding out and crowding in of private donations and government grants. Public Finance Review,42(2), 143–175. https://doi.org/10.1177/1091142112447525ArticleGoogle Scholar
• Hsiao, C. (2007). Panel data analysis—Advantages and challenges. TEST,16(1), 1–22. https://doi.org/10.1007/s11749-007-0046-xArticleGoogle Scholar
• Hsiao, C. (2014). Analysis of panel data. Cambridge University Press. BookGoogle Scholar
• Hutcheson, G. D., & Sofroniou, N. (1999). The multivariate social scientist: Introductory statistics using generalized linear models. SAGE Publications, Ltd. http://methods.sagepub.com/book/the-multivariate-social-scientist
• James, R. N., III. (2018). Cash is not king for fund-raising: Gifts of noncash assets predict current and future contributions growth. Nonprofit Management and Leadership,29(2), 159–179. https://doi.org/10.1002/nml.21334ArticleGoogle Scholar
• Jaskyte, K. (2012). Boards of directors and innovation in nonprofit organizations. Nonprofit Management and Leadership,22(4), 439–459. https://doi.org/10.1002/nml.21039ArticleGoogle Scholar
• Jensen, U. T., & Vestergaard, C. F. (2016). Public service motivation and public service behaviors: Testing the moderating effect of tenure. Journal of Public Administration Research and Theory,27(1), 52–67. https://doi.org/10.1093/jopart/muw045ArticleGoogle Scholar
• Keele, L., & Kelly, N. J. (2006). Dynamic models for dynamic theories: The ins and outs of lagged dependent variables. Political Analysis,14(2), 186–205. https://doi.org/10.1093/pan/mpj006ArticleGoogle Scholar
• Kim, M. (2015). Socioeconomic diversity, political engagement, and the density of nonprofit organizations in US counties. The American Review of Public Administration,45(4), 402–416. ArticleGoogle Scholar
• Kim, Y. H., & Kim, S. E. (2018). What accounts for the variations in nonprofit growth? a cross-national panel study. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations, 29(3), 481–495. https://doi.org/10.1007/s11266-016-9752-x. ArticleGoogle Scholar
• Light, R. J., & Pillemer, D. B. (1984). Summing Up: The Science of Reviewing Research. Harvard University Press. https://books.google.com/books?id=5Y14EDR7UicC
• Maddala, G. S., & Wu, S. (1999). A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics,61(S1), 631–652. https://doi.org/10.1111/1468-0084.0610s1631ArticleGoogle Scholar
• Maier, F., Meyer, M., & Steinbereithner, M. (2016). Nonprofit organizations becoming business-like: A systematic review. Nonprofit and Voluntary Sector Quarterly,45(1), 64–86. ArticleGoogle Scholar
• Matsunaga, Y., Yamauchi, N., & Okuyama, N. (2010). What determines the size of the nonprofit sector?: a cross-country analysis of the government failure theory. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations, 21(2), 180–201. https://doi.org/10.1007/s11266-010-9125-9. ArticleGoogle Scholar
• Mayer, W. J., Wang, H., Egginton, J. F., & Flint, H. S. (2014). The impact of revenue diversification on expected revenue and volatility for nonprofit organizations. Nonprofit and Voluntary Sector Quarterly,43(2), 374–392. ArticleGoogle Scholar
• Mosley, J. E., & Galaskiewicz, J. (2015). The relationship between philanthropic foundation funding and state-level policy in the era of welfare reform. Nonprofit and Voluntary Sector Quarterly, 44(6), 1225–1254. https://doi.org/10.1177/0899764014558932. ArticleGoogle Scholar
• Nickell, S. (1981). Biases in dynamic models with fixed effects. Econometrica: Journal of the Econometric Society, pp. 1417–1426.
• Nikolova, M. (2015). Government funding of private voluntary organizations: Is there a crowding-out effect? Nonprofit and Voluntary Sector Quarterly,44(3), 487–509. https://doi.org/10.1177/0899764013520572ArticleGoogle Scholar
• Paarlberg, L. E., & Hwang, H. (2017). The heterogeneity of competitive forces: the impact of competition for resources on united way fundraising. Nonprofit and Voluntary Sector Quarterly, 46(5), 897–921. https://doi.org/10.1177/0899764017713874. ArticleGoogle Scholar
• Pandey, S. K., & Johnson, J. M. (2019). Nonprofit management, public administration, and public policy: Separate, subset, or intersectional domains of inquiry? Public Performance and Management Review,42(1), 1–10. https://doi.org/10.1080/15309576.2018.1557382ArticleGoogle Scholar
• Pedrini, M., & Ferri, L. M. (2016). Doing well by returning to the origin. Mission drift, outreach and financial performance of microfinance institutions. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations, 27(6), 2576–2594. https://doi.org/10.1007/s11266-016-9707-2. ArticleGoogle Scholar
• Plümper, T., Troeger, V. E., & Manow, P. (2005). Panel data analysis in comparative politics: Linking method to theory. European Journal of Political Research,44(2), 327–354. https://doi.org/10.1111/j.1475-6765.2005.00230.xArticleGoogle Scholar
• Ranucci, R., & Lee, H. (2019). Donor influence on long-term innovation within nonprofit organizations. Nonprofit and Voluntary Sector Quarterly,48(5), 1045–1065. https://doi.org/10.1177/0899764019843346ArticleGoogle Scholar
• Rao, C. R., & Toutenburg, H. (1995). Linear Models: Least Squares and Alternatives (1st ed.). Springer. https://doi.org/10.1007/978-1-4899-0024-1
• Rosenbaum, P. R. (2005). Heterogeneity and Causality. The American Statistician,59(2), 147–152. https://doi.org/10.1198/000313005X42831ArticleGoogle Scholar
• Rotolo, T., Wilson, J., & Dietz, N. (2014). Volunteering in the United States in the aftermath of the foreclosure crisis. Nonprofit and Voluntary Sector Quarterly,44(5), 924–944. https://doi.org/10.1177/0899764014546669ArticleGoogle Scholar
• Shearer, R., & Clark, T. (2016). Are we drawing the correct conclusions? Regression analysis in the nonprofit literature. Canadian Journal of Nonprofit and Social Economy Research, 7(1). https://doi.org/10.22230/cjnser.2016v7n1a213
• Sydow, J., Schreyögg, G., & Koch, J. (2009). Organizational path dependence: Opening the black box. The Academy of Management Review,34(4), 689–709. Google Scholar
• Szper, R. (2013). Playing to the test: Organizational responses to third party ratings. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations,24(4), 935–952. https://doi.org/10.1007/s11266-012-9290-0ArticleGoogle Scholar
• Tsay, W.-J., & Chung, C.-F. (2000). The spurious regression of fractionally integrated processes. Journal of Econometrics,96(1), 155–182. https://doi.org/10.1016/S0304-4076(99)00056-ArticleGoogle Scholar
• Wawro, G. (2002). Estimating dynamic panel data models in political science. Political Analysis,10(1), 25–48. https://doi.org/10.1093/pan/10.1.25ArticleGoogle Scholar
• Weimar, D., Wicker, P., & Prinz, J. (2015). Membership in nonprofit sport clubs: A dynamic panel analysis of external organizational factors. Nonprofit and Voluntary Sector Quarterly,44(3), 417–436. ArticleGoogle Scholar
• Wicker, P., & Frick, B. (2016). Recruitment and retention of referees in nonprofit sport organizations: the trickle-down effect of role models. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations, 27(3), 1304–1322. https://doi.org/10.1007/s11266-016-9705-4. ArticleGoogle Scholar
• Winters, M. S., & Rundlett, A. (2015). The challenges of untangling the relationship between participation and happiness. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations,26(1), 5–23. https://doi.org/10.1007/s11266-014-9500-zArticleGoogle Scholar
• Witt, A., Kurths, J., & Pikovsky, A. (1998). Testing stationarity in time series. Physical Review E,58(2), 1800–1810. https://doi.org/10.1103/PhysRevE.58.1800ArticleGoogle Scholar
• Wooldridge, J. M. (2005). Fixed-effects and related estimators for correlated random-coefficient and treatment-effect panel data models. Review of Economics and Statistics,87(2), 385–390. ArticleGoogle Scholar
• Wooldridge, J.M. (2013). Introductory Econometrics: A Modern Approach (5th ed.). Cengage Learning. https://books.google.com/books?id=C0KHwUKxys0C
• Woronkowicz, J., & Nicholson-Crotty, J. (2017). The effects of capital campaigns on other nonprofits’ fundraising. Nonprofit Management and Leadership,27(3), 371–387. https://doi.org/10.1002/nml.21255ArticleGoogle Scholar
• Yi, H., & Chen, W. (2019). Portable innovation, policy wormholes, and innovation diffusion. Public Administration Review,79(5), 737–748. https://doi.org/10.1111/puar.13090ArticleGoogle Scholar
• Yu, Z. (2016). The effects of resources, political opportunities and organisational ecology on the growth trajectories of AIDS NGOs in China. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations,27(5), 2252–2273. https://doi.org/10.1007/s11266-016-9686-3ArticleGoogle Scholar
• Zhu, L. (2013). Panel data analysis in public administration: Substantive and statistical considerations. Journal of Public Administration Research and Theory,23(2), 395–428. https://doi.org/10.1093/jopart/mus064ArticleGoogle Scholar

Funding

This study was not funded by any funding/grants.